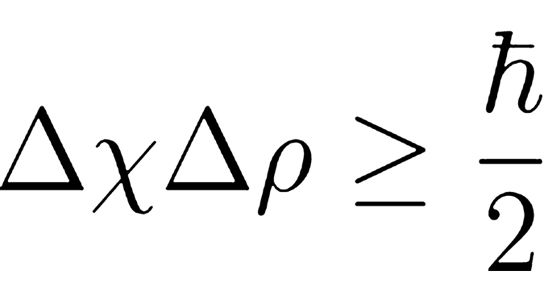Heisenberg restriction garners a significant update. One of the foundations of quantum theory is an elemental restriction to the accuracy with which we can assimilate specific pairs of physical quantities like position and momentum.
For quantum conceptual treatment, the uncertainty concepts are formulated in the context of Heisenberg restriction which permits for physical quantities that do not possess analogs observable in the management of quantum mechanics like time and energy or the phase remarked in interferometric computations. It places a rudimentary restriction on measurement precision in terms of the resources utilized. At present, an alliance of researchers in Poland and Australia has demonstrated that the Heisenberg restriction as it is usually expressed is not functionally consequential and varies from the accurate restriction by a factor of π.
The Heisenberg restriction can be viewed as a purified alternative of the Heisenberg unpredictability connection adjusted for the motivation of quantum estimation theory and quantum metrology describes Wojciech Gorecki the lead author.
Quantum metrology makes use of quantum effects like entanglement for escalated resolve, escalated susceptibly calculations and as Gorecki indicates, the Heisenberg restriction regularly emerges in this field when considering with the states constituting several probable entangled investigations.
Here the Heisenberg restrictions signify a qualitative enhancement over calculation strategy that does not enforce entanglement. The Heisenberg uncertainty principle goes back to Heisenberg’s efforts in Copenhagen in 1927 and albeit absolute when it initially came up, it is presently well ensconced in literature and research depending on quantum theory.
Steve Lopez is the Editorial Page Editor for News Raise. He covers Health. He has won more than a dozen national journalism awards for his reporting and column writing at seven newspapers and four news magazines.